Functions

Activation Function

The activation function is used to determine the output of the neuron. It's called an activation function, because the result is either that the neuron lights up, or it doesn't.

Each hidden layer has its own activation function, which passes information from the previous layer into the next one.

• Once all the outputs from the hidden layers are generated, then they are used as inputs to calculate the final output of the neural network

The activation function of a current node is applied to the weighted sum of all nodes of the previous layer to that current node, plus the bias. That is:

activation of a node $= \sigma(w_{1}a_{1} + w_{2}a_{2} +...+ w_{n}a_{n} + b)$

• $\sigma$ - activation function (e.g. Sigmoid, ReLU)
• $w$ - weight of connection
• $a$ - activation level of previous layer's node
• $b$ - bias

The most common activation function is ReLU, but historically Sigmoid was also used.

The Activation Functions can be basically divided into 2 types:

1. Linear Activation Function
2. Non-linear Activation Functions
   • most common

Loss Function (a.k.a Cost Function/Error Function)

A loss function tells us how far off the output of a neural network is from the real-world expectation. As a result, the purpose is to tell us how well the neural network is performing and provide a value that can be used to update the model's parameters during the training process.

Loss functions enable the model to learn from the training data by minimizing the discrepancy between predictions and ground truth.

• By iteratively adjusting the model's parameters to minimize the loss function, the model improves its ability to make accurate predictions.

The goal during training is to minimize the output of the loss function by adjusting the model's parameters.

To get the value of the loss function, for each output node, we take the difference between its activation value and the value we expected to have, square it, then add them all up.

• the closer the result is to ideal, the lower the sum will be.

In the below example, the results of the model are shown in the yellow-outlined layer. We see that the model incorrectly predicted the number $3$, thereby resulting in a high value from the loss function.

It's important to remember that this loss function involves an average over all of the training data, meaning if we minimize the output of the function, it means it's a better performance on all of that sample data.

When we talk about a network "learning", all we mean is that the network is just minimizing the output of its loss function.

The loss function takes as input all the weights/biases of the network's neurons, and outputs a single number (the measure of how effective the model was)

The gradient of the loss function tells us how to alter the weights/biases cause the fastest change to the output of the loss function

• in other words, it answers the question "which changes to which weights matter the most?"

In Pytorch, the term criterion may be used to refer to a loss function.

Loss functions

• Mean Absolute Error & Mean Square Error - used for regression problems (therefore, predicting a number)
• Cross Entropy Loss - used with classification problems

Mean Absolute Error (MAE)

The below image shows the first stage of our model. It gives us:

• our training data (blue)
• our ideal testing data (green), ie. what the model should ideally predict
• our initial (random) prediction

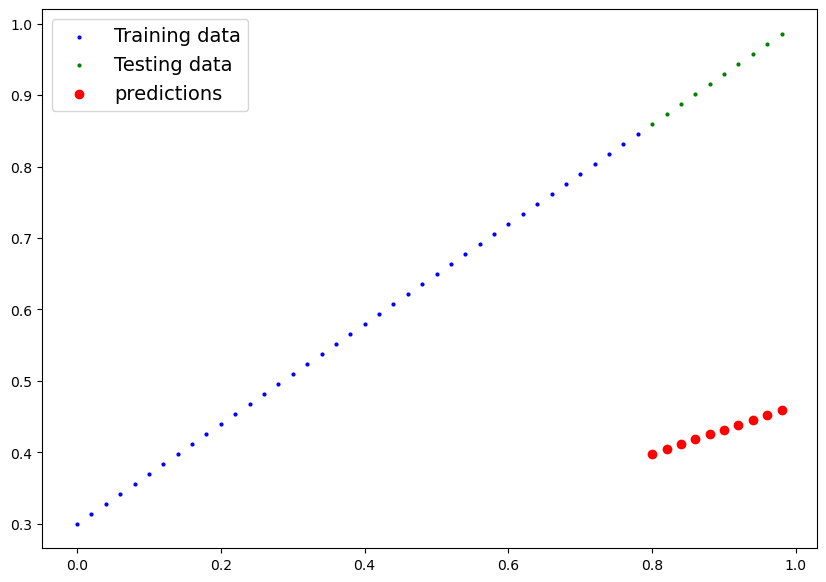
If we were using a Mean Absolute Error loss function, what we would essentially do is get the distance between each red dot and its corresponding green dot (say the first is 0.4 difference), then get the mean of that difference amongst all of the dots. This would be our Mean Absolute Error, and the result of our loss function.

• note: In Pytorch, the MAE loss function is nn.L1Loss

Optimization Algorithm (a.k.a Optimizer)

The optimization algorithm is responsible for updating the model's parameters iteratively based on the gradients of the loss function.

The optimization algorithm aims to find the set of parameter values that minimizes the loss function, leading to improved model performance.

The loss function and optimization algorithm work hand in hand during training. The loss function provides a measure of how well the model is doing, and the optimization algorithm guides the updates of the model's parameters to minimize the loss function.

Gradient Descent

Gradient descent is an example of an optimization function.

• The main objective of gradient descent is to find the parameters (like the weights in a neural network) that minimize the loss function.

Gradient descent is the process of repeatedly nudging an input of a function by some multiple of the negative gradient, and it's a way to converge upon some local minimum of a loss function (demonstrated as a valley in the graph below).

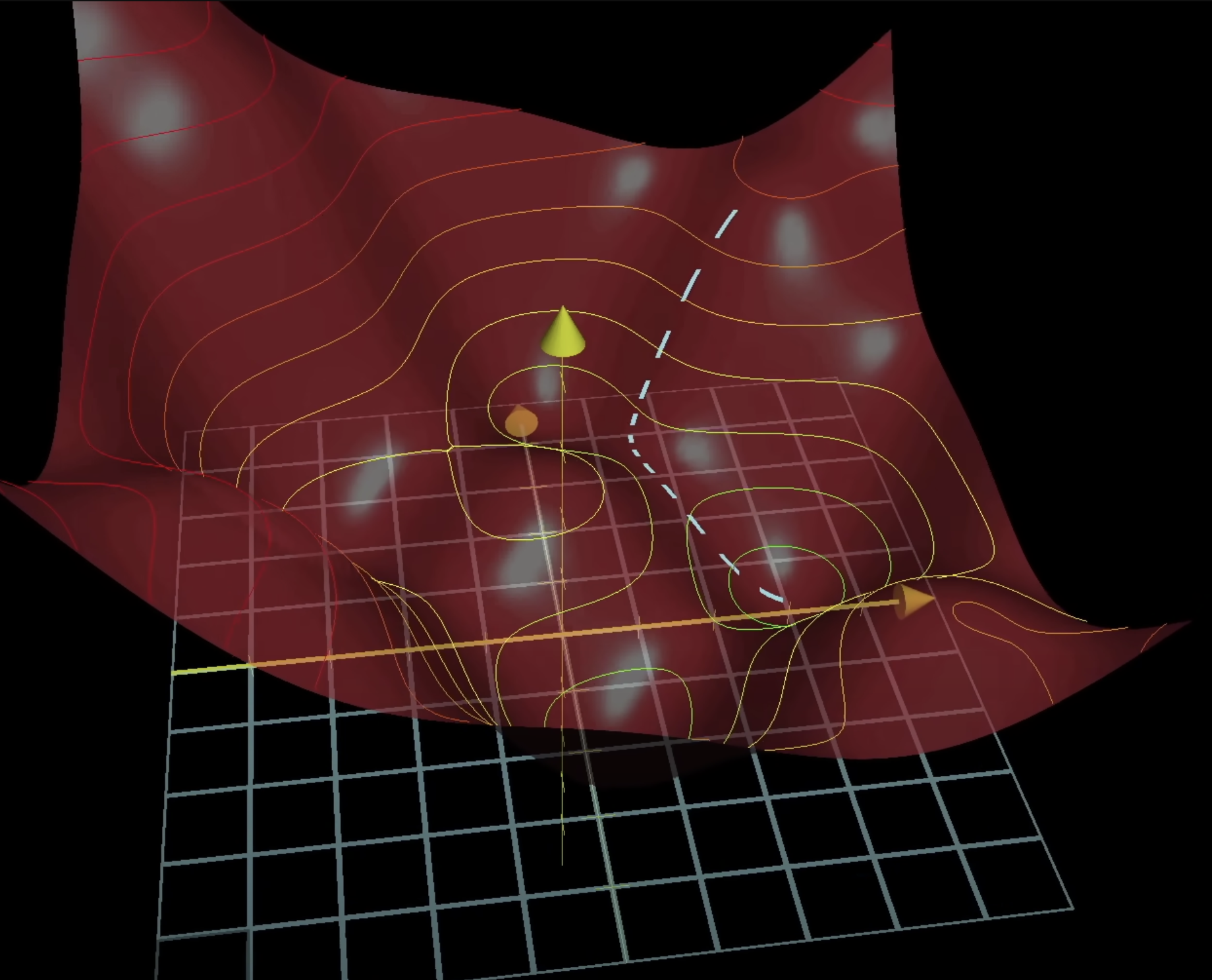
An important note to understand about gradients is that it is reasonably easy to find a local lowest point, but it is difficult to find the global lowest point.

Hyperparameters

see Hyperparameters

• Learning Rate - the higher the learning rate, the more it adjusts each of the model's parameters with each iteration of the model (ie. each time the optimization function gets called)

Backpropagation

Backpropagation is the algorithm used in supervised learning for computing the gradient efficiently. This is effectively the heart of how a neural network learns.

• It involves calculating the gradients of the loss with respect to the network's parameters (weights and biases).
  • This is achieved by applying the chain rule of calculus.
• The gradients tell us how much each parameter should be adjusted to minimize the loss.

Given a neural network and a loss function, the backpropagation calculates the gradient of the error function with respect to the neural network's weights.

• it does this by performing a backward pass to adjust the network model's parameters, aiming to minimize the mean squared error (MSE).

The "backwards" part of the name stems from the fact that calculation of the gradient proceeds backwards through the network, with the gradient of the final layer of weights being calculated first and the gradient of the first layer of weights being calculated last.

Backpropagation is short for "backward propagation of errors"

---

Backlinks

• Machine Learning