Binary

Each node has at most 2 children (referred to ask left child and right child).

We can break a binary tree down into the left subtree and the right subtree.

Binary Search Tree (BST)

A binary tree is a BST if:

• the key of each node in the left subtree is less than all the nodes in the right subtree
• the root key is between the largest key in the left subtree and the smallest key in the right subtree
  • in other works, the root key serves as the dividing point.

The following binary tree is a BST, because there are no nodes in the left subtree that are greater than any node in the right subtree.

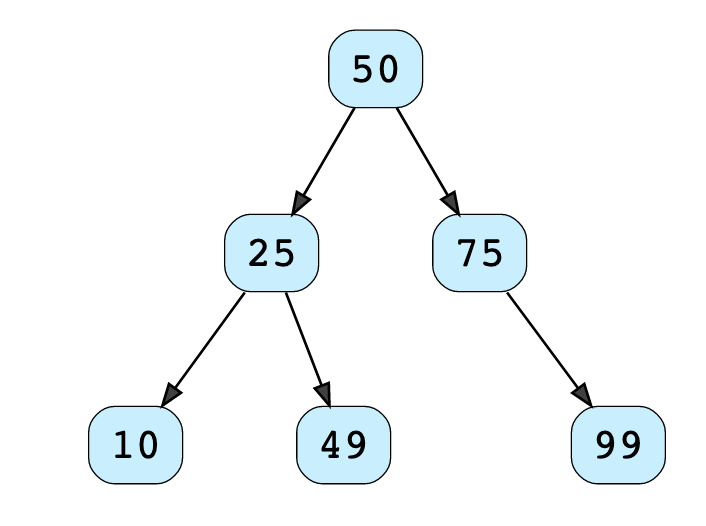
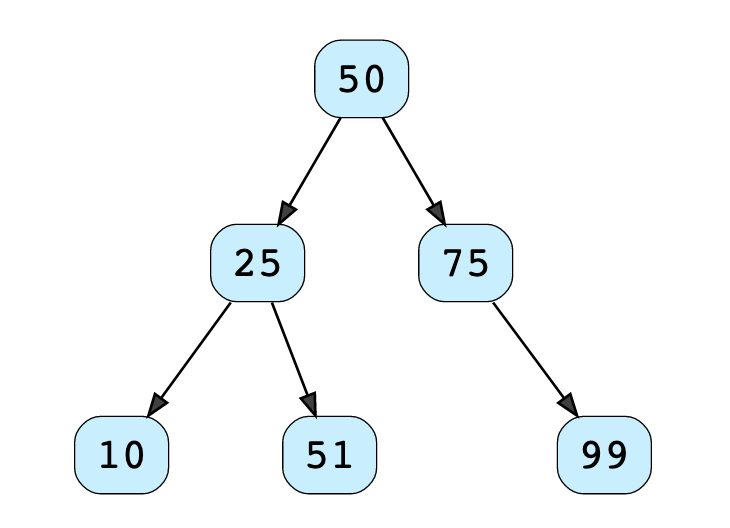
The following binary tree is not a BST, since there is a node with key 51 in the left subtree of 50 which breaks our invariant.

Implementing a BST in Typescript

class TreeNode<T> {
  left: TreeNode<T> | null;
  right: TreeNode<T> | null;
  data: T;

  constructor(data: T) {
    this.left = null;
    this.right = null;
    this.data = data;
  }
}

class BinarySearchTree<T> {
  root: TreeNode<T> | null;

  constructor() {
    this.root = null;
  }

  insert(data: T) {
    const newNode = new TreeNode(data);

    if (!this.root) {
      this.root = newNode;
      return;
    }

    let currentNode = this.root;
    while (true) {
      if (data < currentNode.data) {
        if (!currentNode.left) {
          currentNode.left = newNode;
          return;
        }
        currentNode = currentNode.left;
      } else {
        if (!currentNode.right) {
          currentNode.right = newNode;
          return;
        }
        currentNode = currentNode.right;
      }
    }
  }

  search(data: T): TreeNode<T> | null {
    let currentNode = this.root;

    while (currentNode) {
      if (data === currentNode.data) {
        return currentNode;
      } else if (data < currentNode.data) {
        currentNode = currentNode.left;
      } else {
        currentNode = currentNode.right;
      }
    }

    return null;
  }
}

const bst = new BinarySearchTree<number>();
bst.insert(5);
bst.insert(3);

Finding a node by key

1. Compare current node's key with X. If it's equal, we've found the key. All done.
2. If X is less than node's key, we start looking at node's left subtree. It's because we know that right subtree cannot contain anything greater than X.
3. If X is greater than node's key, we start looking in the right subtree.
4. We repeat this process until we find the key or we reach the leaf node. If we reach the leaf node and haven't found the key as yet, we return not found.

Inserting into tree

New nodes are always leaf nodes. Following the logic of left children being smaller and right children being larger, we start searching a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.

• Therefore, there is only one correct location for the node to be, which is dependent on the key.

Assume we want to insert a node with key K. Starting at the root,

1. Compare current node's key with k.
2. If k is less than the current node,
   • If left child of current node is null, we insert k as the left child of current node and return.
   • If the left child is not null, the left child becomes the new current node, and we repeat the process from step 1.
3. If k is greater than the current node,
   • If right child of current node is null, we insert k as the right child of the current node and return.
   • If the right child is not null, the right child becomes the new current node, and we repeat the process from step 1.

Advantages

Binary trees are useful for accessing nodes based on their key or value. When labelled like this, we can implement a Binary Search Tree (for efficient searching/sorting/min/maxing).

Binary search trees allow binary search for fast lookup, addition and removal of data items, and can be used to implement dynamic sets and lookup tables.

• with the way that the nodes of a BST are arranged, each comparison skips ~half the remaining tree.
  • this results in a time complexity that is logarithmic (O(log n)), making it much faster than the linear time required to find items in an unsorted array, but slower than finding items in a hash table.

Traversal types

• In-order traversals are performed on each node by processing the left subtree, then the node itself, then the right subtree.
• Pre-order traversal
• Post-order traversal

"Storing" a BST

store both Inorder and Preorder traversals. This solution requires space twice the size of Binary Tree.

---

Backlinks

• Heap
• B-tree