B-tree
Unlike a Binary Tree, a B-tree allows more than 2 children per node.
The B-tree is well suited for storage systems that read and write relatively large blocks of data, such as disks.
- Therefore, it is commonly used in databases and file systems.
B-trees keep key-value pairs sorted by key, which allows efficient key- value lookups and range queries.
B-trees break the database down into fixed-size blocks or pages, traditionally 4 KB in size (sometimes bigger), and read or write one page at a time.
- This design corresponds more closely to the underlying hardware, as disks are also arranged in fixed-size blocks.
- Each page can be identified using an address or location, which allows one page to refer to another—similar to a pointer, but on disk instead of in memory. We can use these page references to construct a tree of pages
- in this example, we are looking for the key 251, so we know that we need to follow the page reference between the boundaries 200 and 300. That takes us to a similar-looking page that further breaks down the 200–300 range into subranges. Eventually we get down to a page containing individual keys (a leaf page), which either contains the value for each key inline or contains references to the pages where the values can be found.
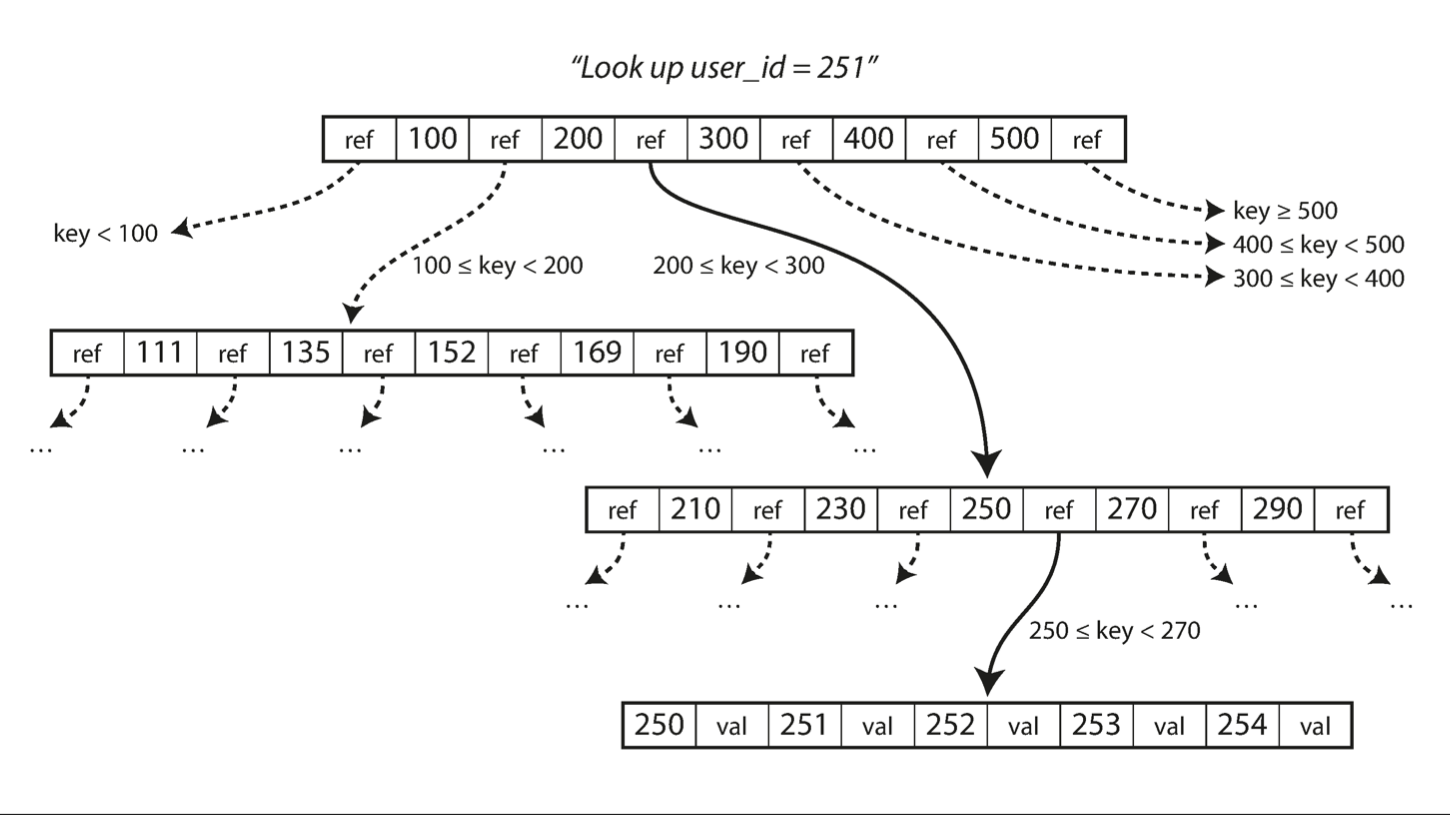
One page is designated as the root of the B-tree; whenever you want to look up a key in the index, you start here.
- The page contains several keys and references to child pages. Each child is responsible for a continuous range of keys, and the keys between the references indicate where the boundaries between those ranges lie.
The number of references to child pages in one page of the B-tree is called the branching factor.
- ex. in the above example, the branching factor is six.
- the branching factor depends on the amount of space required to store the page refer‐ ences and the range boundaries, but typically it is several hundred.
Writing
Inserting a new key into a B-tree is reasonably intuitive, but deleting one (while keeping the tree balanced) is somewhat more involved
The basic underlying write operation of a B-tree is to overwrite a page on disk with new data.
- the overwrite does not change the location of the page
- You can think of overwriting a page on disk as an actual hardware operation. On a magnetic hard drive, this means moving the disk head to the right place, waiting for the right position on the spinning platter to come around, and then overwriting the appropriate sector with new data.
In order to make the database resilient to crashes, it is common for B-tree implementations to include a WAL (write-ahead log).
- When the database comes back up after a crash, this log is used to restore the B-tree back to a consistent state
If you want to update the value for an existing key in a B-tree, you search for the leaf page containing that key, change the value in that page, and write the page back to disk
If you want to add a new key, you need to find the page whose range encompasses the new key and add it to that page.
If there isn’t enough free space in the page to accommodate the new key, it is split into two half-full pages, and the parent page is updated to account for the new subdi‐ vision of key ranges
The B-tree algorithm ensures that the tree remains balanced: a B-tree with n keys always has a depth of O(log n)
- Most databases can fit into a B-tree that is three or four levels deep, so you don’t need to follow many page references to find the page you are look‐ ing for.
- A four-level tree of 4 KB pages with a branching factor of 500 can store up to 256 TB.
A B-tree index must write every piece of data at least twice: once to the write-ahead log, and once to the tree page itself (and perhaps again as pages are split)
Implementation
Backlinks