Space and Time Complexity

Space vs Time

"space can be reused, while time can't."

"Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform."

Space complexity

a function describing the amount of memory that an algorithm takes in terms of input to the algorithm.

• Space complexity is sometimes ignored because the space used is minimal and/or obvious, but sometimes it becomes as important an issue as time.

ex. we might say "this algorithm takes constant extra space," because the amount of extra memory needed doesn't vary with the number of items processed.

Time complexity

a function describing the amount of time an algorithm takes in terms of the amount of input to the algorithm.

• "Time" can mean...
  • the number of memory accesses performed,
  • the number of comparisons between integers,
  • the number of times some inner loop is executed,
  • or some other natural unit related to the amount of real time the algorithm will take.
• We try to keep this idea of time separate from "wall clock" time, since many factors unrelated to the algorithm itself can affect the real time

ex. we might say "this algorithm takes n2 time," where n is the number of items in the input.

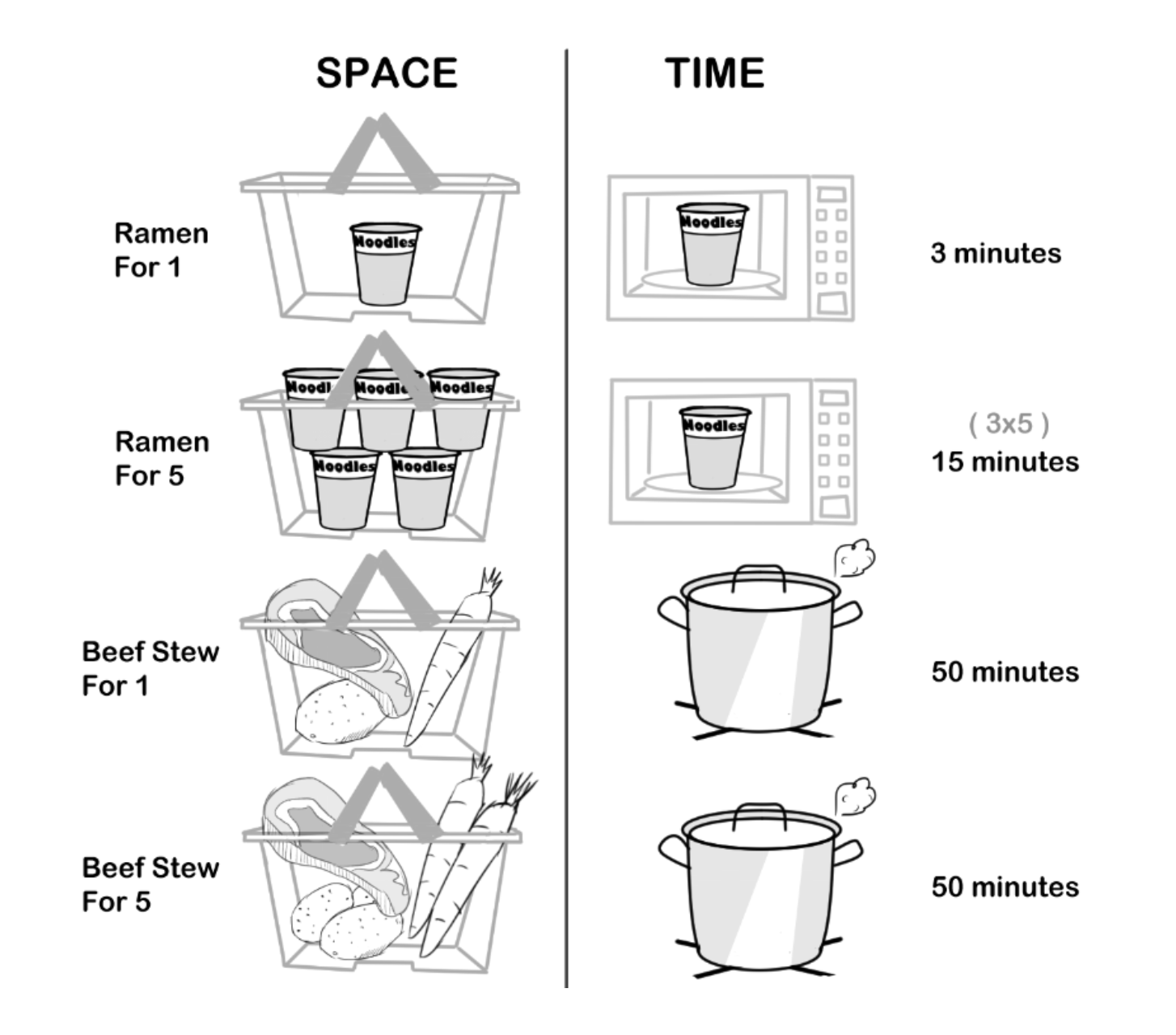
Analogy: Ramen noodles vs. Stew

Consider that if making one cup of ramen noodles takes 3 min, making 5 cups would take 15 min (3x5). Conversely, if I was going to make a beef stu, if one serving takes 50 min, 5 servings will still be roughly 50 min. This is the concept of time. Now consider, that ramen has a 1:1 relationship with space. In other words, if I am filling up a shopping cart, the amount of ramen that takes up space is directly proportional to the number of serving I have to make. 5 servings = 5 cups of ramen noodles. On the other hand, stu for 1 person or 5 will have a less linear relationship. This is the concept of space.

• We want to build algorithms that are more like the stu.

And in mathematical terms... The above shows how the left side of the equation is time/space, and the right side is the O Notation

Time and Space Complexity at this level describe the relationship between Inputs and rate of operations/space taken

Big O

Based on the above, ramen noodles have a time complexity of O(n). In other words, their "growth" rates are linear, and each additional operator will add an a period of time that is equal to the average durations of each operator.

Cases (listed from best to worst):

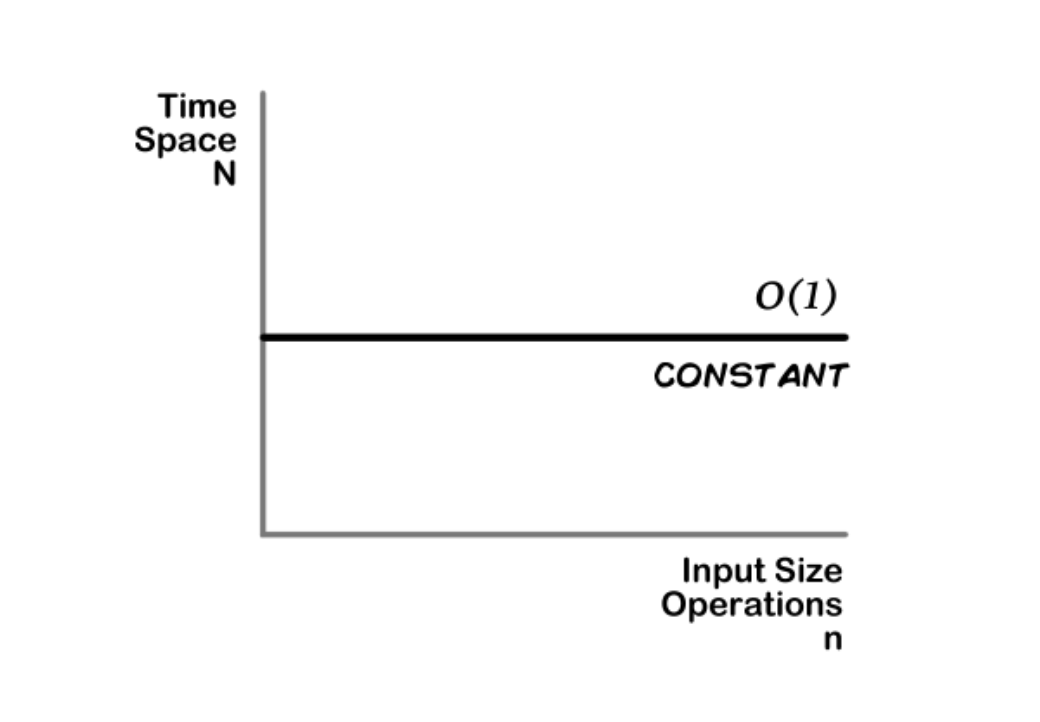
Constant; $O(1)$

It takes at most the same amount of time or space for one or man

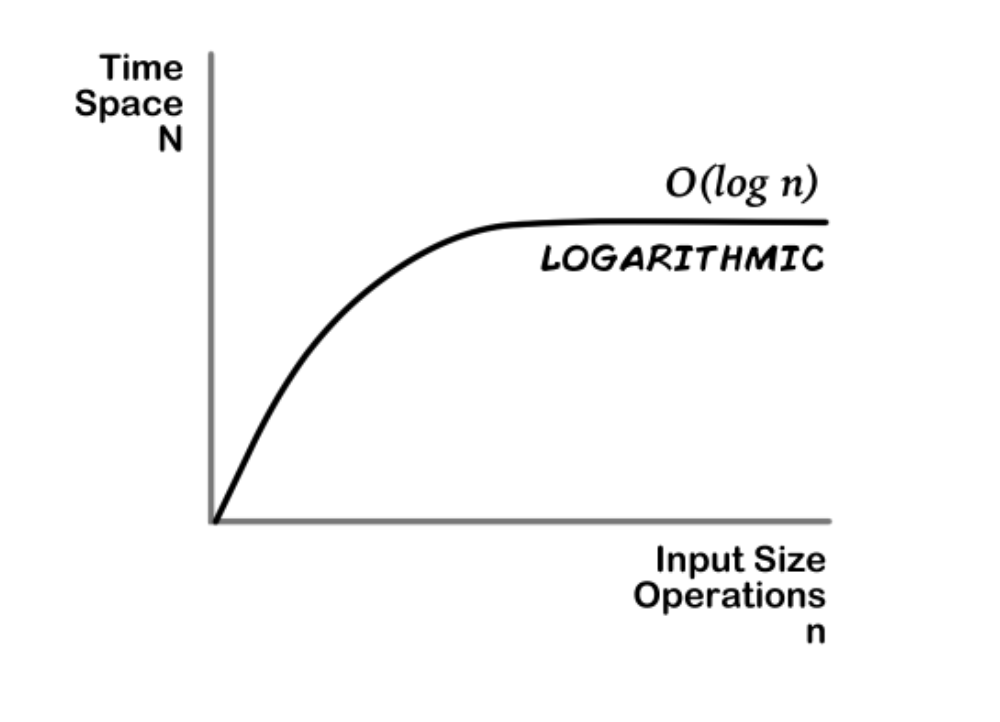
Logarithmic; $O(\log n)$

time and space complexity increases at first but then it stabilizes and changes less

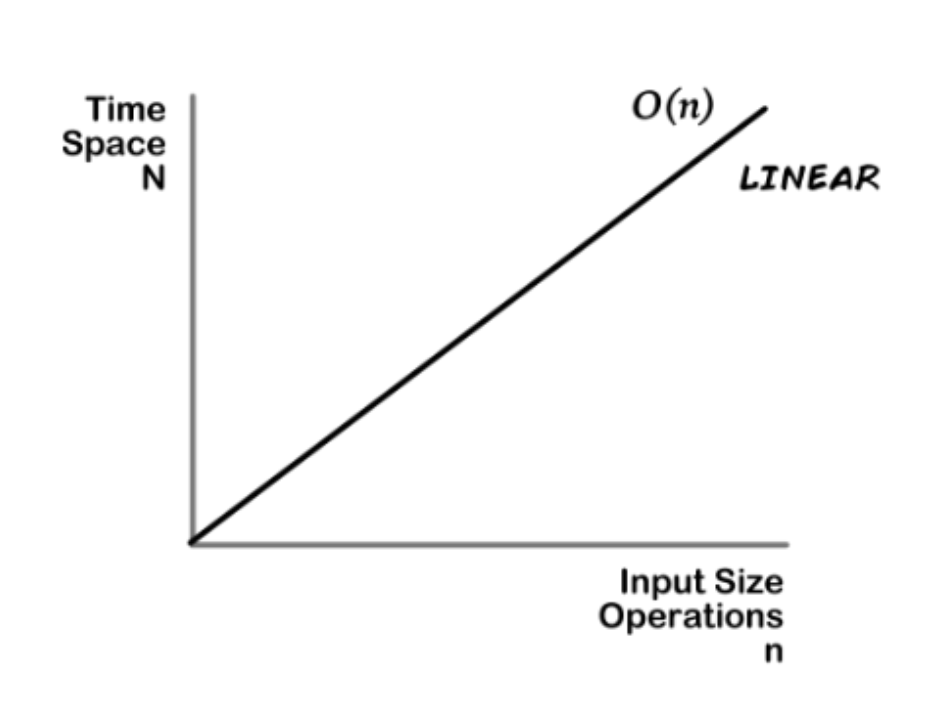
Linear; $O(n)$

here time and space increase at worst at a fixed/liner rate :

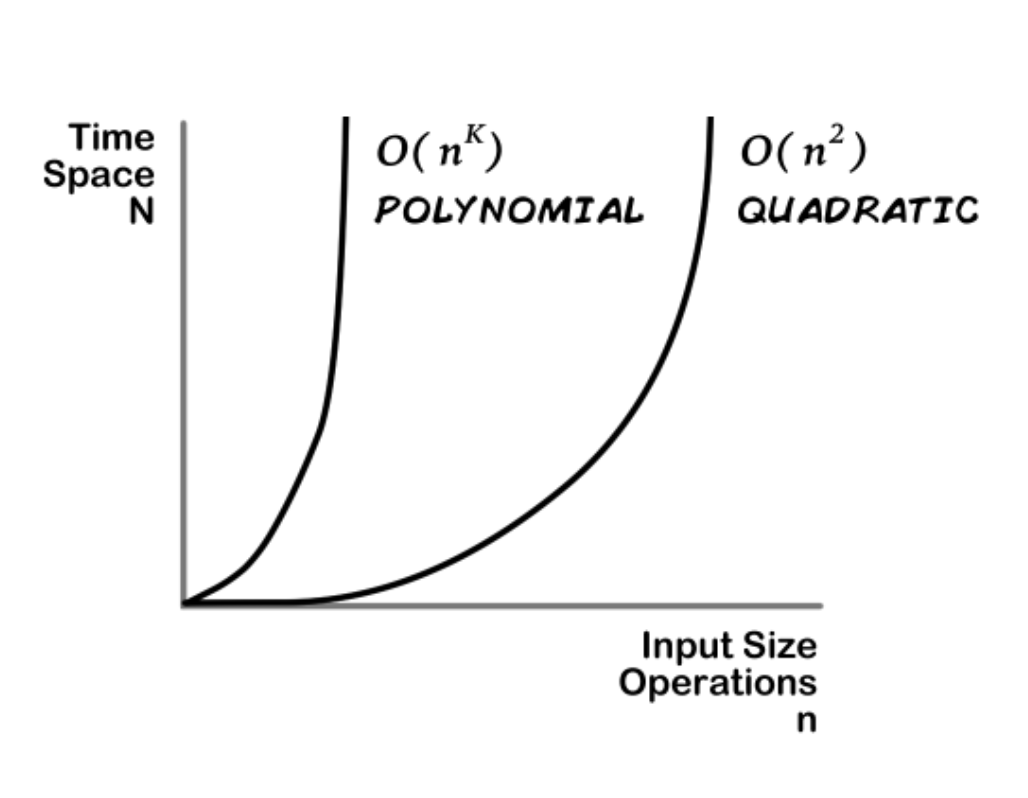
Quadratic & Polynomial

In general as your inputs increase your, time becomes greater at a certain greater rate which is related to the exponent, ^2 for quadratics, ^K for Polynomials and everything in between:

Exponential

rapidly increases until time and space requirements tend towards the infinite.

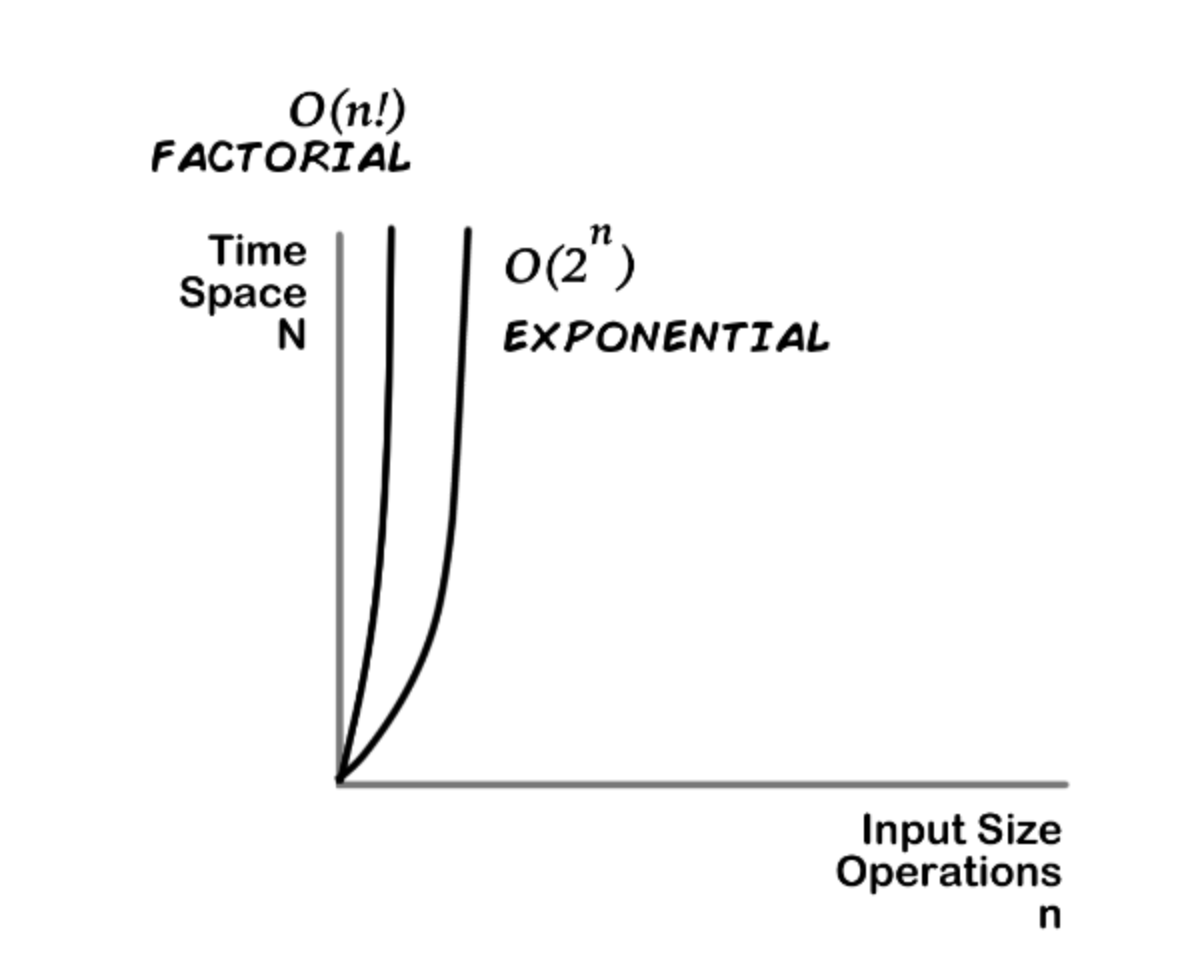
Any time you have a nested loop, where each loop is $O(n)$, you are working with an $O(n)^2$ complexity.

• ex. Nested loops may not be readily apparent. In the following code, we have an .includes() method inside a loop. The time complexity can be considered as $O(n) * O(n) = O(n^2)$, because we are potentially iterating through one string for each character in the other string.

for (const letter of word1AsArray) {
  if (!word2AsArray.includes(letter)) {
    return false;
  }
}

Resources

• Find O-notations of common things, like arrays, objects etc

---

Backlinks

• Binary
• Trie