Neural Network

Overview

Neural networks are preferred when you have unstructured data (ie. data that is not neatly formatted in tables)

that's not to say that they can't work well with structured data. It's more the case that traditional machine learning algorithms like decision trees or SVMs often handle structured data well.

At a basic level, a neural network is comprised of four main components:

inputs
- ex. your inputs may have a binary value of 0 or 1
weights - Larger weights make a single input’s contribution to the output more significant
a bias or threshold - the output value of any node must be above the threshold for data to be sent to the next layer of the network
- a threshold value of 5 would translate to a bias value of –5.
an output (y-hat)

Node (a.k.a Neuron)

Each node corresponds to a neuron in a biological neural network

Think of each node as its own linear regression (Private) model.

since linear regression can be used to predict future events

Think of a neuron as a function that takes in the outputs of all nodes from the previous layer and returns a number between 0 and 1.

this number is called the activation, and it is the output of the activation function
the activations in one layer determine the activations in the subsequent layer.
note: While many activation functions produce values between 0 and 1 (like the sigmoid function), not all do. For instance, the ReLU (Rectified Linear Unit) function produces values between 0 and infinity, and the tanh function outputs values between -1 and 1.

Weight

Each connection between 2 nodes is assigned a weight, which indicates the strength of that connection, and how much influence the input has on the node.

Each node (the current node) receives input from every node of the previous layer. To each of these inputs we apply a weight that affects how much of a contribution that particular node of the previous layer has on the current node

Weight is a fundamental concept to neural networks because inputs naturally have a different magnitude of effort on the outcome

ex. in a model that predicts housing prices, the recency of a paint job and the number of bedrooms are both inputs to the model that affect the price, but the latter has a much bigger impact on the ultimate price of the house.

Weights are the primary mechanism by which neural networks learn. During training, the network gets feedback on its predictions in the form of a loss or error. To minimize this error, the model uses optimization techniques (like gradient descent) to adjust the weights. Over time, the model gradually makes more and more accurate predictions.

The main difference between regression (Private) and a neural network is the impact of change on a single weight.

In regression, you can change a weight without affecting the other inputs in a function. this isn’t the case with neural networks. Since the output of one layer is passed into the next layer of the network, a single change can have a cascading effect on the other neurons in the network.

The neural network figures out the weights on its own

a.k.a representation, patterns, numbers, features

Bias

The bias is a value that is applied to the weighted sum of all neurons from the previous layer, adjusting the importance of that neuron.

In other words, the bias gives us some indication of whether or not that neuron tends to be active or inactive.
More specifically, bias shifts the activation function along the input axis, essentially determining the threshold at which the neuron begins to activate.

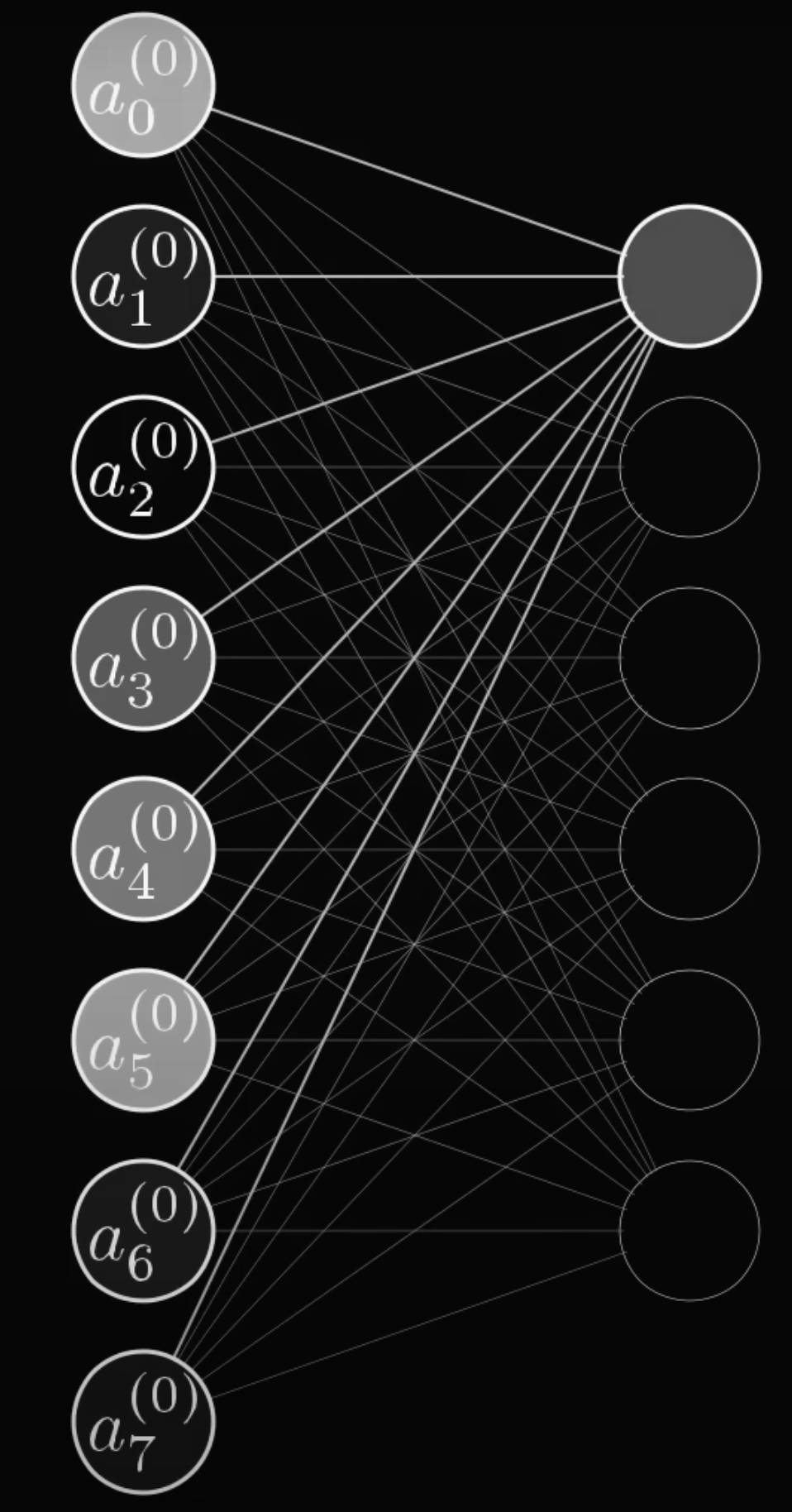
Layers

Neural networks are composed of layers. Generally they are:

input layer
hidden layers
output layer

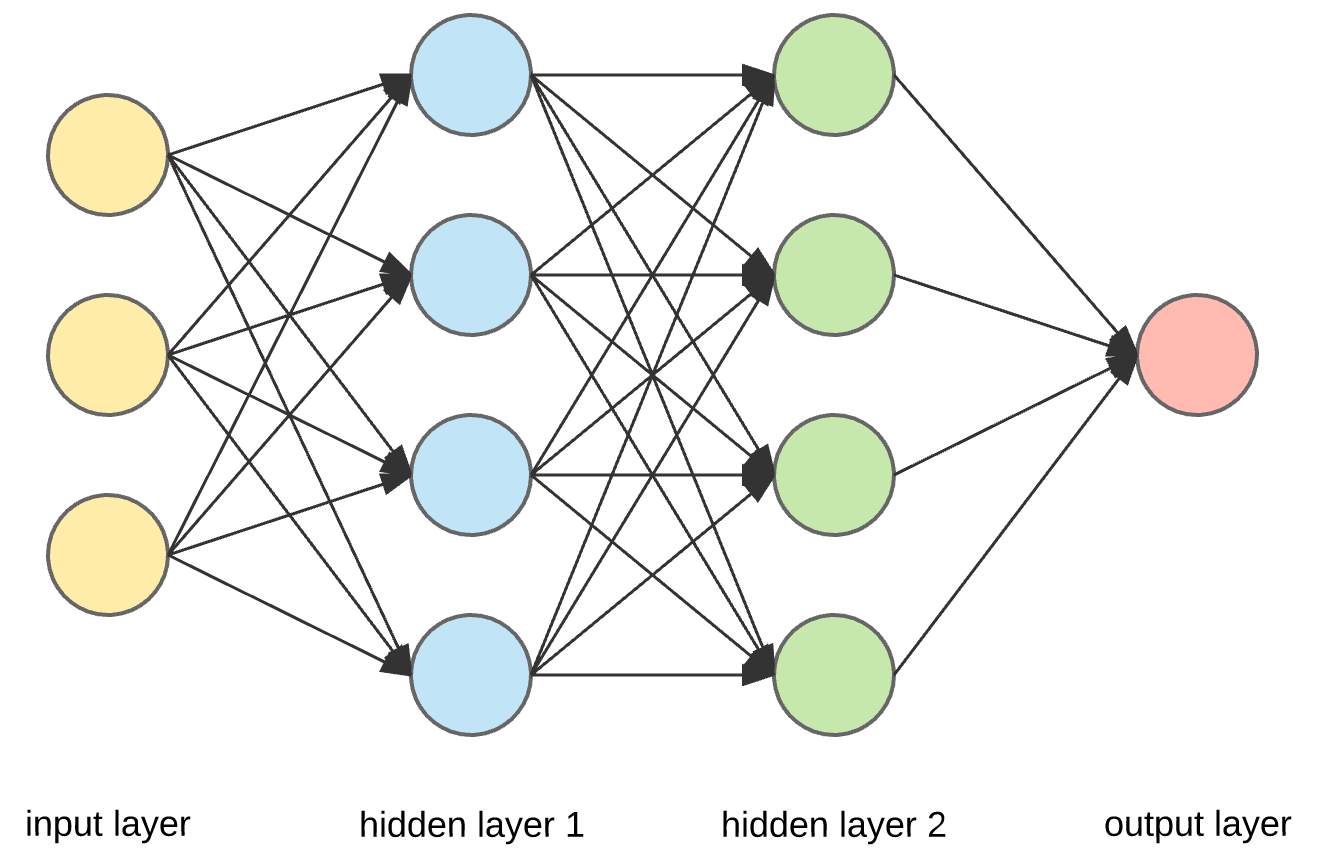
Each layer is usually a combination of linear functions (ie. straight lines) and non-linear functions (ie. non-straight lines)

How a neural network learns (simplified)

A neural network learns by:

starting with random numbers
perform tensor operations
update random numbers to try and make them better representations of the data
repeat

Types of Neural Network

From Types

Go to text →

Data is passed from one layer to the next in what's called a Feedforward neural network (FNN)

so-called because connections between the nodes do not form a cycle.

Other types of Neural Network:

Convolutional Neural Networks (CNNs) are commonly used as the model architecture in image classification tasks
Recurrent Neural Networks (RNNs) are commonly used in natural language processing tasks
Transformer are commonly used in natural language and speech
Fully Connected Neural Networks (FCNN)

Example: number recognition

Imagine we have a model that takes an image (28x28 pixels) of a handwritten number and tells us what number it is.

First layer - Our neural network will start with 784 neurons ( $28x28$ ), and each value between 0 and 1 will represent its grayscale level (from black to white). These 784 neurons make up the first layer of our neural network.
Last layer - Our last layer will be composed of 10 neurons, each representing a digit from 0-9.
Hidden layers - Though hidden layers are a black box, it helps to think of them in terms of how they might behave. Generally when solving problems with computers, it's helpful to break problems down into smaller problems, then use the smaller building block solutions to amount to a bigger solution. In this case, it's difficult to recognize the number $9$ . However, it's easier to recognize a shape with a loop and a tail (the top and bottom part of the number, respectively). There are however, different numbers that have loops ( $6$ , $8$ , $0$ ) and different numbers that have tails ( $7$ , $1$ ). So we might think, "What if each node in our second last layer represented a different component shape? Then the activation functions of the loop node and the tail node would output a number close to 1, which would be enough information to tell us that we have the number $9$ ".
- of course, then the question becomes "how do we recognize shapes like loops and tails?". We can continue to break down these shapes to reveal straight-ish edges. That is, we can think of the upper loop of the number $9$ as being made up of ~5 straight-ish edges. When our neural network receives the handwritten $9$ , it can break it down first into edges, then determine which shapes those edges make, and then finally determine which number it is based on which shapes it has found.
- video demonstration

The activation of these neurons (often simply a number between 0-1) represents how much the model thinks that the input image is that particular number

ex. if our input drawing was of a 9, then the final neuron in the last layer will have the highest activation value

In this example, the weights of each node activation tell us the pixel pattern that that node is picking up on, while the bias tells us how high the weighted sum needs to be before we consider the neuron to be meaningfully active