Recursion

In general, recursive code helps us avoid complex nested loops and is most useful for tasks that can be defined in terms of similar subtasks.

Each recursive function consists of 2 parts:

1. Base Case: The base case is where further calls to the same function stop, i.e, it does not make any subsequent recursive calls.
2. Recursive Case: The recursive case is where the function calls itself again and again until it reaches the base case.
   • Each child function call returns result to its parent function.

Both recursion and iteration depend on a condition which determines whether to stop execution or continue it.

Methods to understand flow of recursive function

Visualizing through a stack

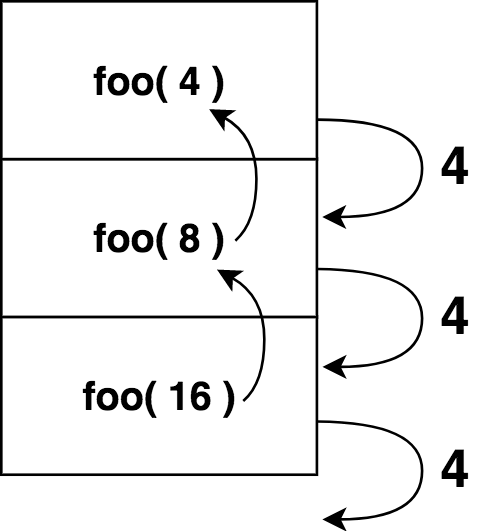
The concept of a stack is critical in recursion. When you start visualizing your function calls through a stack and how it returns when reaching a base case - the concept of recursive calls and their output becomes easier to comprehend.

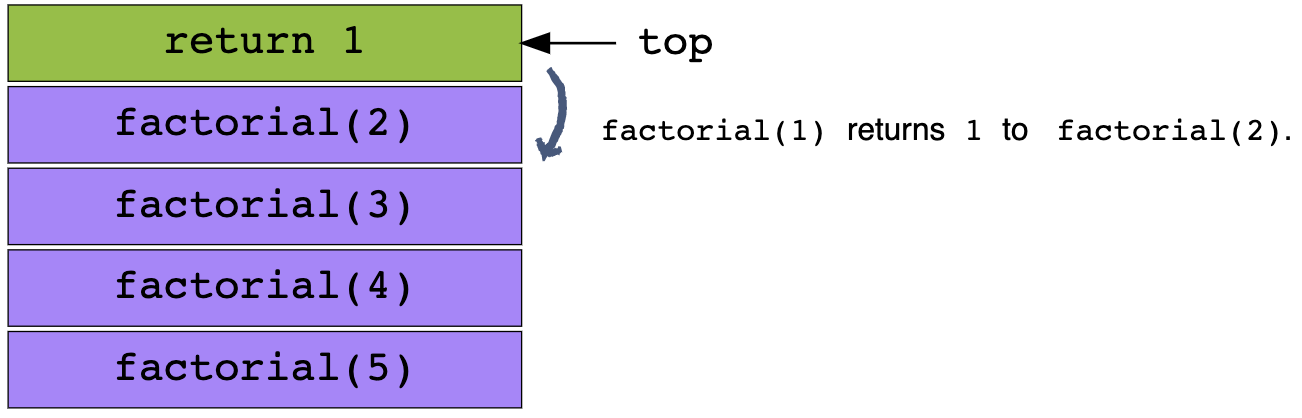
Recursing: 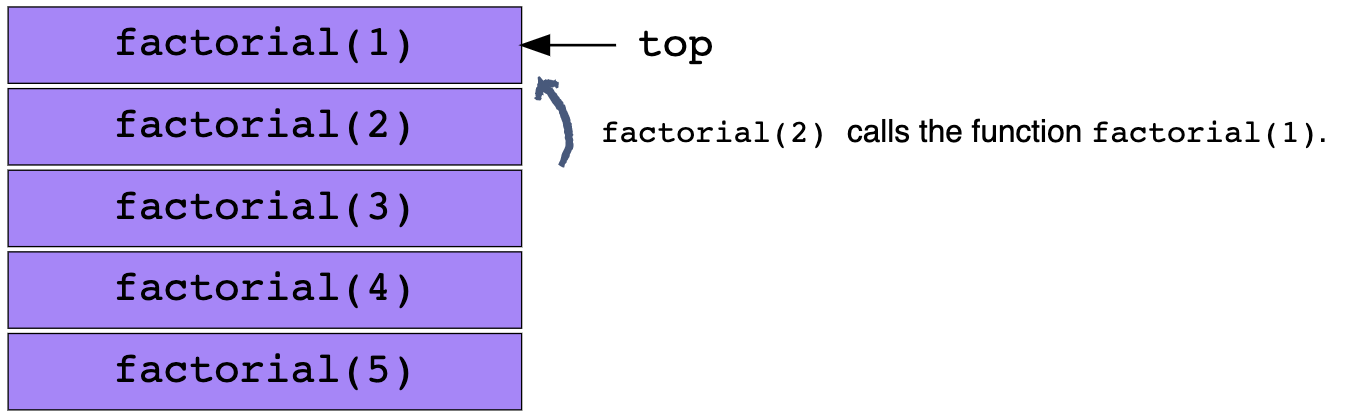Returning values to lower stacks:

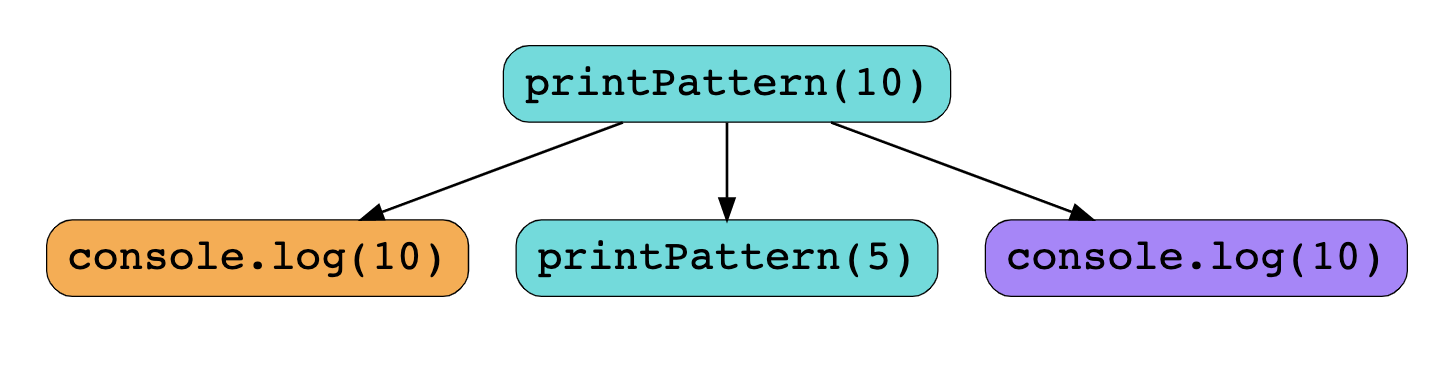
Making a recursive tree

Consider that each function call must return before subsequent code can be run. In the first recursive step (ie. "iteration 1"), the recursing function does not actually return until the base-case is complete. In fact, it is the final call of that function to actually return.

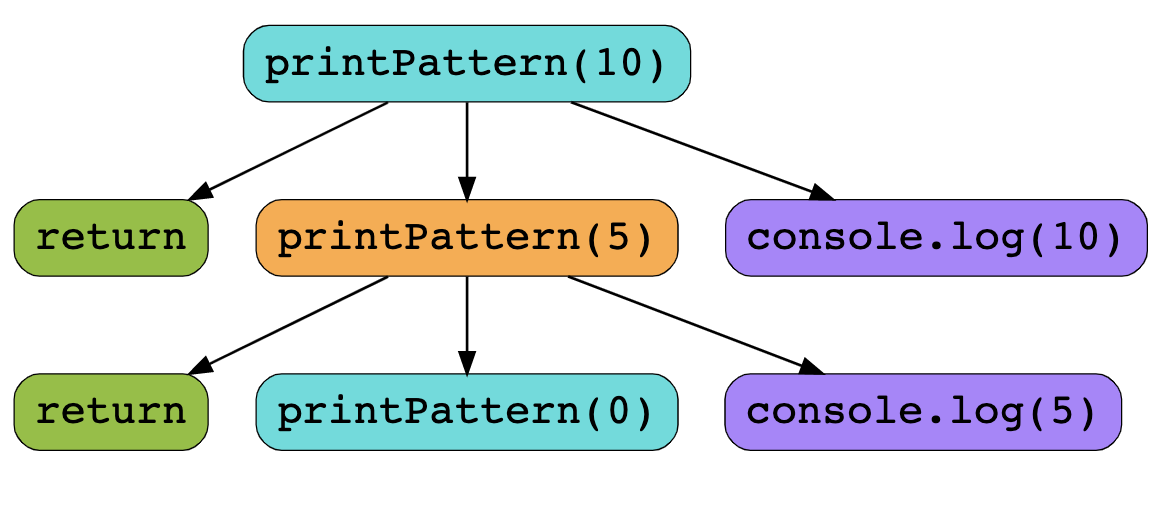
Parallels with mathematics

Mentally, what's happening is similar to when a mathematician uses a Σ summation in a larger equation. We're saying, "the max-even of the rest of the list is calculated by maxEven(...restNums), so we'll just assume that part and move on."

function maxEven(num1, ...restNums) {
	var maxRest = restNums.length > 0 ? maxEven(...restNums) : undefined;

	return (num1 % 2 != 0 || num1 < maxRest) ? maxRest : num1;
}

console.log(maxEven(1, 6, 3))

Once the base case is met, the final return value makes its way back up all layers of the call stack to give us that value

function foo(x) {
    if (x < 5) return x;
    return foo( x / 2 );
}

Recursion is declarative for algorithms in the same sense that Σ is declarative for mathematics.

using reverseString as an example:

function reverseString(string) {
  // Base case
  if (string === "") {
    return string;
  }

  // Recursive case
  else {
    // take the last character and add it to the reverse of the previous characters
    return string[string.length - 1] + reverseString(string.substr(0, string.length - 1));
  }
}

spec: consider what we are doing here, conceptually. We are taking the last character, putting it at the front, and calling the function again with the last character popped off. Each time we recurse, we build up the new string. That is, each "iteration" adds one character to the new string. That whole idea can be summed up with just this part of the function: string[string.length - 1] + ... (ie. the first part of the return value). Assuming you understand the logic taking place each "iteration" (ie. get the last character of a truncated (by one character) string), then you don't really need to focus on the recursive-function-call part of the return value. This logic taking place is reflected in the value that is passed to the recursive function. Once you've internalized this, then you can inherently understand the values you are working with. Given string[string.length - 1] + ..., we know that we are just adding the last character to the front.

1. Cook