For full text search please use the '?' prefix. e.g. ? Onboarding

Tensors

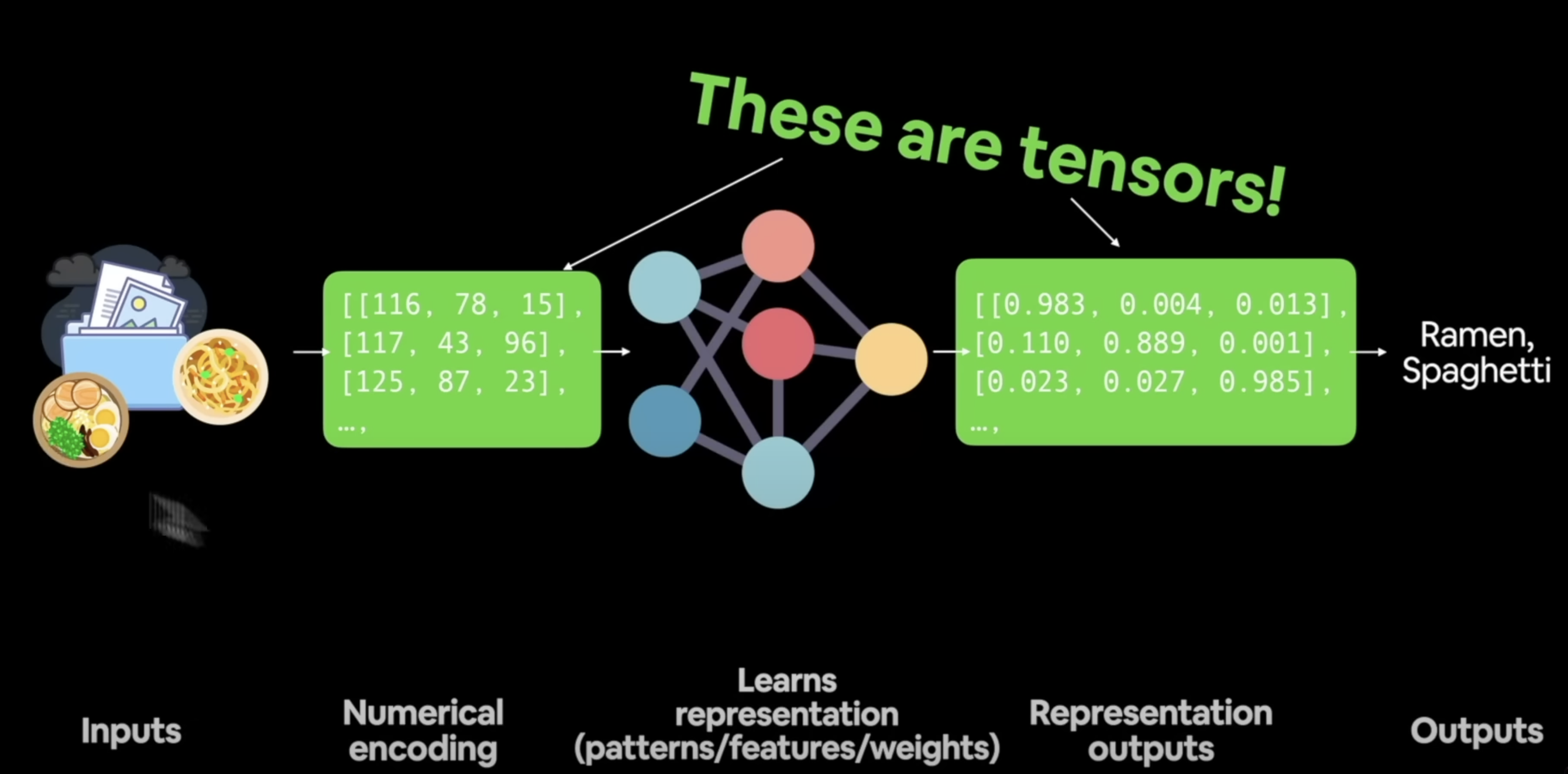
Tensors are the primary data structure used for representing and manipulating data in deep learning models.

  • they are the numerical representation of data as it is used as an input to the model, and it is also the numerical representation that is output by the model (ie. representation outputs)
    • therefore, the inputs and outputs of a neural network are tensors
  • ex. Imagine we have a machine learning model that predicts if an image is of a shirt or not. In this case, the tensors would typically hold the image data in the form of numerical values. The image data is represented as pixel intensities, which can be transformed into tensors.
    • if we consider what an image is, it's simply an assortment of pixels, where each pixel is some combination of RGB. If we had a pixel art of Mario which was 16x12, then we could create a tensor of shape (16, 12, 3), where the first dimension represents the height, the second represents the width, and the third represents the color channel (ie. each pixel's degree of RGB). With this tensor, we could recreate the image.

Tensors are often created internally by Pytorch (e.g., the weights of a neural network), but we as developers sometimes create tensors manually, especially when importing data or during preprocessing.

Many neural networks perform their learning by starting off with tensors full of random numbers, and then adjusting those numbers to better represent the data (by taking the source data, such as an image, and encoding its data and replacing the random numbers within the tensor).

  • this is done to help break the symmetry and prevent the model from getting stuck in a suboptimal solution.
  • it also helps with reinforcement learning algorithms in order to introduce exploration during the learning process. By adding random noise to the actions taken by an agent, it can explore different states and actions, enabling it to discover new and potentially better strategies.

Tensors are similar to an ndarray (N-dimensional array), due to certain characteristics:

  • it is multidimensional
    • Tensors can have different dimensions, including 0-dimensional (scalar), 1-dimensional (vector), 2-dimensional (matrix), and higher-dimensional arrays.
  • each element is of the same type
  • each sub-array is of the same (fixed) length

The main difference between a tensor and an ndarray is that a tensor can run on GPUs and TPUs, in addition to CPUs

The variable for tensors that are 0 or 1 dimension (ie. scalars or vectors) is lowercase, while the variable for tensors that are more than 2 (ie. matrices and tensors) is UPPERCASE.

Tensor attributes

A tensor on PyTorch has attributes:

Shape

the size of the tensor; ie. the size of each layer of nested []

  • ex. a tensor of shape [2, 3, 4] would have 2 elements in its outermost brackets, each of which would have 3 elements (ie. 3 arrays), and each element of that array would have 4 elements:
[
    [
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 8, 7, 6]
    ],
    [
        [9, 8, 7, 6],
        [5, 4, 3, 2],
        [1, 2, 3, 4]
    ]
]
  • TENSOR.shape (or alias TENSOR.size())

Data Type

the type of data stored in the tensor

  • TENSOR.dtype
  • default is float32
  • convert type: TENSOR.type(torch.float32) OR TENSOR.to(torch.float32)

Device

the device in which the tensor is stored

  • TENSOR.device
  • default is cpu
  • moving tensor from CPU to GPU: TENSOR.to('cuda:0')

Gradient Requirement

the state of whether or not gradients need to be computed for the tensor

- `TENSOR.requires_grad`
  • spec: gradient is the same as slope if we are considering a straight line in a graph

Tensors on the CPU and NumPy arrays can share their underlying memory locations, and changing one will change the other.

data = [[1, 2],[3, 4]]
x_data = torch.tensor(data)

Tensor Manipulation

Tensor Operations

The neural network will combine these tensor operations in some way in order to find patterns in numbers of a dataset

All operations (except matrix multiplication) are element-wise, meaning the operator (×, ÷ etc.) is applied to each element in place

Operations include:

  • addition
  • subtraction
  • multiplication
    • torch.mul(TENSOR, 10)
  • division
  • matrix multiplication
    • torch.matmul(TENSOR1, TENSOR2) or torch.mm() or TENSOR1 @ TENSOR2
    • matrix multiplication is the most common type of operation found in neural networks
    • see Matrix multiplication (Private) Dendron node

Transpose

Transposing a matrix is simply swapping the row contents with its column contents.

tensor_A
# tensor([[ 7,  8,  9],
#        [10, 11, 12]])
tensor_A.T
# tensor([[ 7, 10],
#        [ 8, 11],
#        [ 9, 12]])

We do this since we cannot multiply two matrices unless # rows of MatrixA = # columns of MatrixB, and # columns of MatrixA = # rows of MatrixB (see rules of matrix multiplication (Private)), we need to transpose one of our matrices if the shapes don't line up properly.

Tensor Aggregation (tensor methods)

Finding the .min(), .max(), .mean(), .sum() etc. of certain tensor values.

Reshaping, Stacking, Squeezing and Unsqueezing Tensors

Each of these methods allows us to manipulate our tensors in order to change their shape/dimension.

  • we often use these to solve issues that might arise due to tensors with mismatched shapes.

  • Reshaping - reshapes an input tensor to a defined shape

    • we do this because in order for multiple tensors to work together, we need their shape to correspond to one another
    • the new shape of the reshaped tensor must be compatible with the original tensor
      • ex. if we have a tensor [1, 2, 3, 4, 5, 6], we cannot reshape it into a 2x2 tensor. We could however put it into a 2x3.

  • View - return a view of an input tensor of certain shape, but keep the same memory as the original tensor

    • therefore if we assign a new variable Z to the view of an existing tensor and then change Z, it will also change the original tensor

  • Stacking - combine multiple tensors, either on top of each other (vstack) or side-by-side (hstack)

  • Squeeze - removes all 1 dimensions from a tensor

    • 1 dimension is a dimension (ie. an array) has a single element in it
    • ex. if we have a tensor of shape [2, 1, 2, 1, 2] and squeeze it, it will become [2, 2, 2]

  • Unsqueeze - add a 1 dimension to a target tensor

    • we must specify the dim argument, which specified which index to add

  • Permute - returns a view that rearranges (ie. swaps) the dimensions of a tensor in a specified way

    • ex. if we have a tensor (x) of shape (2, 3, 5) and permute it as (2, 0, 1), the new tensor will have shape (5, 2, 3)

Indexing

Sometimes you'll want to select specific data from tensors

  • ex. only the first column or second row.

Aside from how indexing normally works (e.g. using [0][0] to access first element of the first element), we can also use : to specify "all values in this dimension"

x = tensor([[1, 2, 3],
            [4, 5, 6],
            [7, 8, 9]])

# Get all values of 0th dimension and the 0 index of 1st dimension
x[:, 0] # tensor([[1, 2, 3]])

# Get all values of 0th & 1st dimensions but only index 1 of 2nd dimension
x[:, :, 1] # tensor([[2, 5, 8]])

# Get all values of the 0 dimension but only the 1 index value of the 1st and 2nd dimension
x[:, 1, 1] # tensor([5])

# Get index 0 of 0th and 1st dimension and all values of 2nd dimension (same as x[0][0])
x[0, 0, :] # tensor([1, 2, 3])

# Get the first 10 values of the 0 dimension
x[:10]

# Get all values after the 10th index
x[:10]

Resources

see tensors Dendron node for mathematical definition (Private)