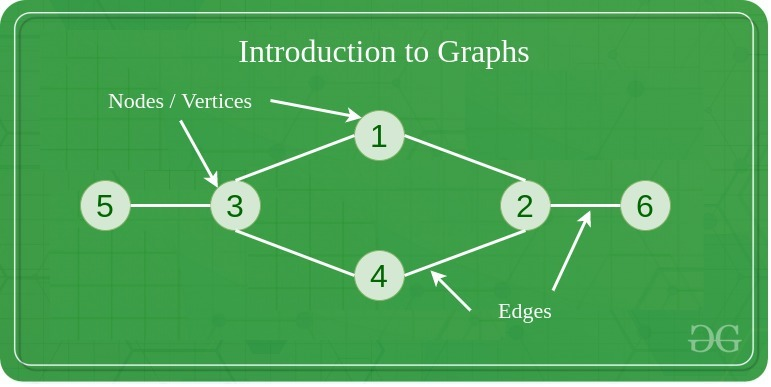
Graph

A Graph is a non-linear data structure consisting of nodes (a.k.a vertices) and edges.

• the node is the fundamental unit of the graph
• the edge is used to connect 2+ nodes

When to use a graph

Graphs offer benefits as a data structure in situations where you need to represent and analyze relationships between objects or entities.

Examples include:

• social networks, where each node represents a person and each edge represents a connection between two people, such as a friendship or a follower/following relationship.
• computer networks, where each node represents a device and each edge represents a connection between two devices, such as a wired or wireless connection.
• transportation systems, where each node represents a location and each edge represents a route between two locations, such as a road or a rail line.
• Recommendation engines, where each node represents an item and each edge represents a relationship between two items, such as a similarity or a co-occurrence.

Types of graph

Directed graph (a.k.a digraph) vs Undirected graph

A directed graph is a graph in which the edges have a direction.

Cyclic graph vs Acyclic graph

A cyclic graph is a graph that includes at least one cycle, whereby you can start at one node and follow a path to end up back at the same node.

• A cyclic graph can be either directed or undirected.

Examples of cyclic graphs include:

• social networks. If Alex, Kyle and Elizabeth are all friends with each other, then what results is a cyclic graph

Examples of acyclic graphs include:

• decision trees, whereby each node represents a decision/outcome of a decision, and each edge represents a causal relationship between one decision and the next
• dependency systems, where each node represents a dependency, and each edge represents one dependency depending on another.
  • assuming no circular dependencies. If there are, then it is cyclic.

Implementing a graph in Typescript

type Vertex<T> = {
  data: T;
  edges: Edge<T>[];
};

type Edge<T> = {
  source: Vertex<T>;
  target: Vertex<T>;
  weight?: number;
};

class Graph<T> {
  private vertices: Vertex<T>[];

  constructor() {
    this.vertices = [];
  }

  addVertex(data: T): Vertex<T> {
    const vertex: Vertex<T> = { data, edges: [] };
    this.vertices.push(vertex);
    return vertex;
  }

  addEdge(source: Vertex<T>, target: Vertex<T>, weight?: number): Edge<T> {
    const edge: Edge<T> = { source, target, weight };
    source.edges.push(edge);
    return edge;
  }

  getAdjacentVertices(vertex: Vertex<T>): Vertex<T>[] {
    return vertex.edges.map((edge) => edge.target);
  }
}

const graph = new Graph<string>();

const a = graph.addVertex('A');
const b = graph.addVertex('B');
const c = graph.addVertex('C');

graph.addEdge(a, b);
graph.addEdge(b, c);
graph.addEdge(c, a);

const adjacentVertices = graph.getAdjacentVertices(a);

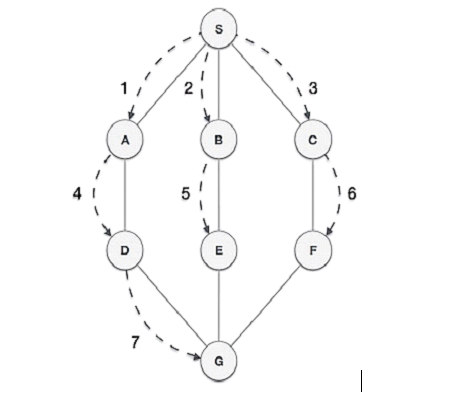
BFS and DFS

BFS and DFS are types of graph traversal algorithms

BFS (Breadth First Search)

used to find the shortest path in the graph between two nodes.

start from the top node in the graph and travels down until it reaches the root node

uses a queue to remember how to get the next vertex to start a search, in the event that a dead end occurs in any iteration.

• therefore, FIFO

BFS is slower and requires a large memory space.

BFS is better when target is closer to Source.

// represents an adjacency list, where each key represents a vertex and the corresponding value is an array of its neighbors.
type Graph = {
  [key: string]: string[];
};

function bfs(graph: Graph, startNode: string): string[] {
  // store the vertices that need to be visited.
  const queue = [startNode];
  const visited: { [key: string]: boolean } = {};
  const result: string[] = [];

  // run until the queue is empty
  while (queue.length > 0) {
    // remove first vertex in queue and store in `currentNode`
    const currentNode = queue.shift()!; // `!` assert value is truthy, since `.shift()` can return undefined if queue is empty
    if (!visited[currentNode]) {
      visited[currentNode] = true;
      result.push(currentNode);
      for (const neighbor of graph[currentNode]) {
        queue.push(neighbor);
      }
    }
  }

  // returns an array of visited vertices in the order they were visited.
  return result;
}

const graph: Graph = {
  A: ['B', 'C'],
  B: ['D', 'E'],
  C: ['F'],
  D: [],
  E: ['F'],
  F: []
};

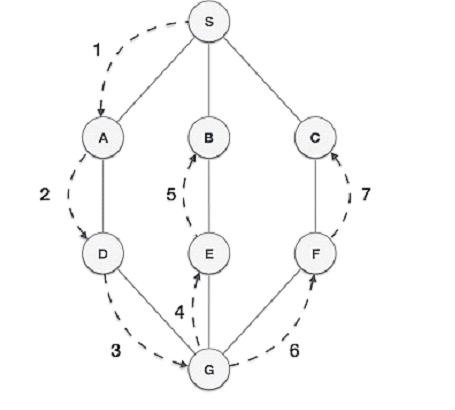
DFS (Depth First Search)

start from the top node and follows a path to reaches the end node of the path.

uses a stack to remember how to get the next vertex to start a search, in the event that a dead end occurs in any iteration.

• therefore, LIFO

DFS is faster and requires less memory.

DFS is best suited for decision trees.

Terminology

Path

A path in a graph is a finite or infinite set of edges which joins a set of nodes.

• therefore, a path must have a starting node
• if the path connects all the nodes of a graph data structure, then it is a connected graph, otherwise it is called a disconnected graph.
• There may or may not be path to each and every node of graph. In case, there is no path to any node, then that node becomes an isolated node.